今回は情報科学系の方向け.
次元削減のいち手法である「Random Projection」を簡単に紹介します.
具体的にやってること,できることはものっそ簡単で,こないだBoostアドベ記事を書き上げてから寝付けなかったのでふと思い立って取り組んでみたら一発ですごいちゃんとできたのでブログにまとめるに至った次第(そしてその日はそのまま寝付けずに昼間死ぬかと思ったという).
最初に知ったのはMIRU2011という,夏にあった学会でとある論文を読んだ時.
もちろんわかってると思いますが,ツッコミ待ちです!!
次元削減とは
機械学習やデータ処理あたりの用語で,高次元データをその情報をなるべく保ったまま低次元に変換するタスクやその技術を指します.
具体的な手法として主成分分析(PCA)や特異値分解(SVD)あたりはこの分野の院生クラスなら必須教養レベルって言ってもいいんじゃなかろか.
Random Projection
Random Projectionでできること
一言で言うと,「超高次元空間に分布する点群を,互いの距離関係を高い確率で保ったまま低次元空間に写像する」ことができる手法.
距離関係を保つと言うのは,例えば次元ベクトルを
次元に写像する変換
(つまり
行列)があるとき,
次元点群
について
に最も近い点が
,遠い点が
だったなら,写像後の点群を見ても
に最も近い点は
だし遠い点は
になる,ということです.このことを言い換えると,「空間の構造を保ったまま低次元化する」ことになります.
距離関係すなわち空間の構造を保ったまま低次元化できると,例えば部分空間に基づく分類問題の解法として有名なk-NNなどを写像後の点群に適用しても等価であるとみなしてよいことになり,計算コストが低減できたりするわけです.
で実際どうするか
原理としては魚が死ぬぐらいシンプルで,その次元から
次元に写像する行列
の要素を乱数で設定する,というだけ.びっくり.
設定する値としては,ささっと探した範囲では以下の3通りがあるみたい.
- [-1,1]の一様乱数
- N(0,1)の正規乱数
- 1/6の確率で
,1/6の確率で
,残りは
(以下ヘルシンキと呼びますw)
イイところ
なんと言っても同じような目的に使う他の手法に比べて計算量が圧倒的に少ないこと.
特に,後の実験でも示せていますが,変換行列はかなり疎な行列でもよくて,このことはさらに効率化できることを意味します(疎行列に特化したデータ構造・アルゴリズムが存在します).
実験1:シミュレーション
実験の考え方
「距離関係を保っている」ことをどう確認するか,です.
次元空間にランダムな
個の点群をplotする
- この点群間の相互の距離を記述した対称行列
を求める
- 全ての点を
によって
次元へ削減した点群をplotする
- この点群についても距離行列
を求める
の各要素を
の対応する要素で割る.すなわち,距離行列を距離変化率行列に変換する
このとき,距離関係を完全に保った写像がなされていれば,距離変化率行列の非対角要素には全て同一の値が入っているはずです.
このばらつき()が小さいほど,距離空間を保てているということになります.
このを平均
で割ることで正規化し,この値
を評価に用います.
例えばが0.04だったら,距離の変化率はだいたい68%が±4%以内に収まってることになります(
区間).
これを,
-
変換行列の生成手法ごとに
- 一様乱数による手法
- 正規乱数による手法
- ヘルシンキでの手法
-
点群の数ごとに
- 100点
- 500点
- 1000点
-
変換前の点の各次元ごとに
- 100次元
- 1000次元
- 10000次元
-
次元の削減割合ごとに
- 1% (ただし変換前が100次元のときは除く)
- 2% ( 〃 )
- 5%
- 10%
- 20%
で試してみます.
実験手法
C++でeigenとboostを使い倒してやります.プログラムは後の方に掲載しますが,かなりシンプル.
でもこういうときMATLABやOctaveやRをヴァリヴァリ使いこなせると強いよなぁ…
高い方の次元数Mと低い方の次元数N,点群の数k,Projection行列の乱数に設定する値を上記の3通りから選び,それぞれ変更できます.
データ点群は,基底ごとに一様乱数で設定することで生成.これが後で少し問題になるのですが.
実験結果例
以下だらだらと長い結果が続きますので,結論から.
-
次元の落とし方があまりに極端でなければ,
は十分小さい
- ゆえに,Random Projectionによって距離関係をかなりよく保ったまま次元を落とせている
の設定の手法による違いはほとんどなさそう
-
さらに,
を,密度10%で要素は[-1:1]の疎行列とした場合も性能は全くおちていない
-
行列ベクトル積の時間はNNZに比例するため密度10%なら10倍を上限に高速化できる
- さらに密度を落としてもかなりいけたけど,若干不安定みたい
-
行列ベクトル積の時間はNNZに比例するため密度10%なら10倍を上限に高速化できる
-
また,ここには載せてないけど,点群の数は無関係
- 当たり前か
 を
を![[-1:1] [-1:1]](https://s0.wp.com/latex.php?latex=%5B-1%3A1%5D&bg=ffffff&fg=000000&s=0) の一様乱数で設定した場合
の一様乱数で設定した場合
- 削減率1%
| M | N(=M*削減率) | |
|---|---|---|
| 1000 | 10 | 0.256491 |
| 10000 | 100 | 0.0723984 |
- 削減率2%
| M | N(=M*削減率) | |
|---|---|---|
| 1000 | 20 | 0.166879 |
| 10000 | 200 | 0.0500503 |
- 削減率5%
| M | N(=M*削減率) | |
|---|---|---|
| 100 | 5 | 0.418443 |
| 1000 | 50 | 0.104068 |
| 10000 | 500 | 0.0317905 |
- 削減率10%
| M | N(=M*削減率) | |
|---|---|---|
| 100 | 10 | 0.252291 |
| 1000 | 100 | 0.0699945 |
| 10000 | 1000 | 0.0224399 |
- 削減率20%
| M | N(=M*削減率) | |
|---|---|---|
| 100 | 20 | 0.168808 |
| 1000 | 200 | 0.0508375 |
| 10000 | 2000 | 0.0159634 |
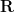 を
を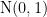 の正規乱数で設定した場合
の正規乱数で設定した場合
- 削減率1%
| M | N(=M*削減率) | |
|---|---|---|
| 1000 | 10 | 0.252391 |
| 10000 | 100 | 0.0714362 |
- 削減率2%
| M | N(=M*削減率) | |
|---|---|---|
| 1000 | 20 | 0.167512 |
| 10000 | 200 | 0.051086 |
- 削減率5%
| M | N(=M*削減率) | |
|---|---|---|
| 100 | 5 | 0.423773 |
| 1000 | 50 | 0.101857 |
| 10000 | 500 | 0.0315046 |
- 削減率10%
| M | N(=M*削減率) | |
|---|---|---|
| 100 | 10 | 0.246678 |
| 1000 | 100 | 0.0714717 |
| 10000 | 1000 | 0.0224643 |
- 削減率20%
| M | N(=M*削減率) | |
|---|---|---|
| 100 | 20 | 0.164085 |
| 1000 | 200 | 0.0507155 |
| 10000 | 2000 | 0.0156286 |
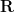 を1/6の確率で
を1/6の確率で ,1/6の確率で
,1/6の確率で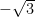 ,残りは
,残りは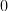 となるよう設定した場合
となるよう設定した場合
- 削減率1%
| M | N(=M*削減率) | |
|---|---|---|
| 1000 | 10 | 0.248877 |
| 10000 | 100 | 0.0720375 |
- 削減率2%
| M | N(=M*削減率) | |
|---|---|---|
| 1000 | 20 | 0.166422 |
| 10000 | 200 | 0.0504729 |
- 削減率5%
| M | N(=M*削減率) | |
|---|---|---|
| 100 | 5 | 0.418621 |
| 1000 | 50 | 0.104153 |
| 10000 | 500 | 0.0318519 |
- 削減率10%
| M | N(=M*削減率) | |
|---|---|---|
| 100 | 10 | 0.252088 |
| 1000 | 100 | 0.071656 |
| 10000 | 1000 | 0.0221902 |
- 削減率20%
| M | N(=M*削減率) | |
|---|---|---|
| 100 | 20 | 0.170909 |
| 1000 | 200 | 0.050107 |
| 10000 | 2000 | 0.0158383 |
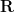 を密度10%の疎行列,非零要素は[-1:1]となるよう設定した場合
を密度10%の疎行列,非零要素は[-1:1]となるよう設定した場合
- 削減率1%
| M | N(=M*削減率) | |
|---|---|---|
| 1000 | 10 | 0.25434 |
| 10000 | 100 | 0.070818 |
- 削減率2%
| M | N(=M*削減率) | |
|---|---|---|
| 1000 | 20 | 0.170246 |
| 10000 | 200 | 0.0502912 |
- 削減率5%
| M | N(=M*削減率) | |
|---|---|---|
| 100 | 5 | 0.430903 |
| 1000 | 50 | 0.102259 |
| 10000 | 500 | 0.0314751 |
- 削減率10%
| M | N(=M*削減率) | |
|---|---|---|
| 100 | 10 | 0.26406 |
| 1000 | 100 | 0.0704771 |
| 10000 | 1000 | 0.0220059 |
- 削減率20%
| M | N(=M*削減率) | |
|---|---|---|
| 100 | 20 | 0.175899 |
| 1000 | 200 | 0.0511966 |
| 10000 | 2000 | 0.0161958 |
シミュレーションでの入力点群,それまずくはないかい?
上で触れたように,データ点群は,基底ごとに一様乱数で設定することで生成してるわけですが,これ少しまずい気がするんですね.
なんででしょう.
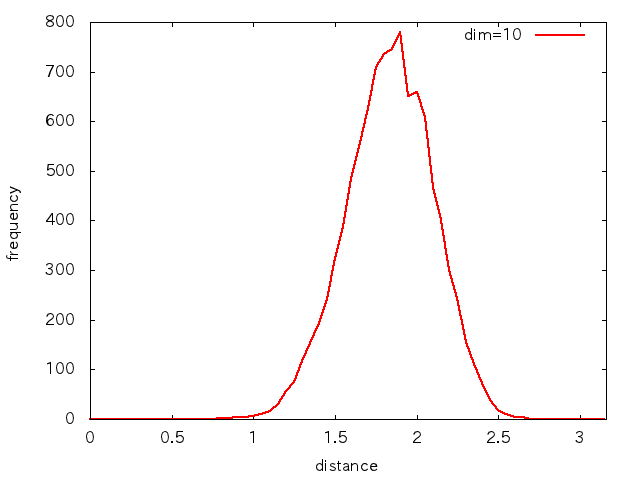
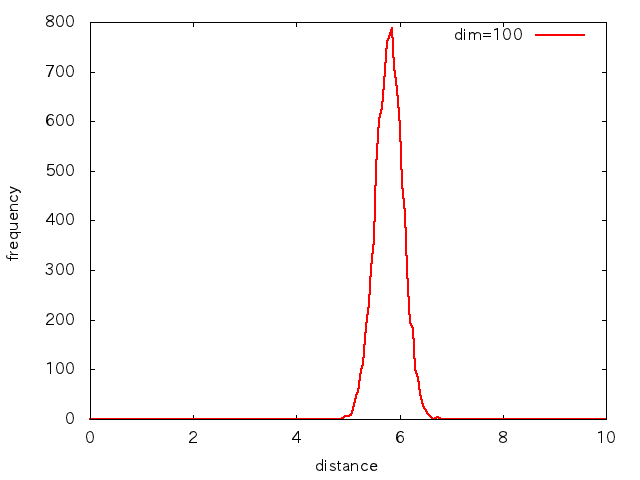
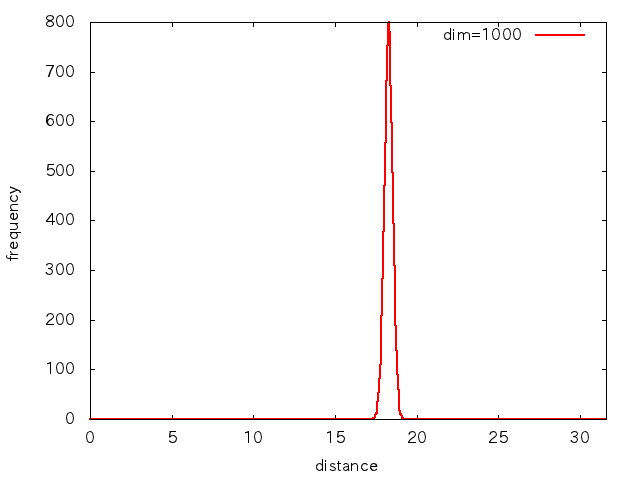
10次元,100次元,1000次元ごとに,各基底が[-1:1]の一様な値をとる10000点からなる点群を用意し,各ベクトルの表す点の原点からの距離でヒストグラムを取ってみると,次のような分布になります.
xrangeは各次元での距離の値域です.
高次元になるほど分布が極端になってきます.
「ほとんど全ての点が,原点からの距離がある一定値」…球面ですね.
ランダムに設定したはずの点が,球面付近に集中してしまうんです.
この理由というのは大学や高専レベルの確率論のお話で,要は,独立な一様乱数の和は正規乱数になって,足す数が増えるほどそのは小さくなるよという話です.
点の各要素は独立な一様乱数なので,原点からのユークリッド距離もおよそ一様乱数の和となっちゃうから(ここ少しだけウソついてますが),距離が正規乱数となるわけです.
2次元以上の空間でなら必ず生じますが,低次元ではが大きいので気づきません.
しかし高次元になると,均等分布しないのです.そしてそれが見えないからタチが悪い.
で,これをどうしたらいいかはよくわからない.
広島大学の玉木先生から助け舟をいただいたりもしているのですが….
[blackbirdpie url=”https://twitter.com/#!/ttttamaki/status/147035480817545216″]
(玉木先生にはほんといつもお世話になっています…w)
シミュレーション実験のプログラム例
170行と若干長いので折りたたんでます.
むしろ170行ですんでるのはすごいかもしらんね.
#include <iostream>
#include <vector>
#include <array>
#include <boost/random.hpp>
#include <boost/accumulators/accumulators.hpp>
#include <boost/accumulators/statistics.hpp>
#include <boost/lexical_cast.hpp>
#include <eigen3/Eigen/Core>
using Eigen::MatrixXd;
using Eigen::VectorXd;
template<class T>
MatrixXd gen_projection_matrix(int N, int D, T& rand)
{
MatrixXd mat(D, N);
for(int i = 0; i < N; i++)
for(int j = 0; j < D; j++)
mat(j, i) = rand();
return mat;
}
std::vector<Eigen::VectorXd> gen_random_points(int N, int num, boost::mt19937& gen)
{
boost::uniform_real<> dst(-100, 100);
boost::variate_generator< boost::mt19937&, boost::uniform_real<> > rand(gen, dst);
std::vector<Eigen::VectorXd> results(num);
std::generate(results.begin(), results.end(), [N, &rand]()
{
Eigen::VectorXd vec(N);
for(int j = 0; j < N; ++j) vec[j] = rand();
return vec;
});
return results;
}
std::vector<Eigen::VectorXd> projection_points(int N, int D, const MatrixXd& projection, const std::vector<Eigen::VectorXd>& srcs)
{
std::vector<Eigen::VectorXd> result(srcs.size());
std::transform(srcs.begin(), srcs.end(), result.begin(),
[projection](const Eigen::VectorXd& vec) { return projection * vec; });
return result;
}
MatrixXd gen_distance_vector(const std::vector<Eigen::VectorXd>& points)
{
const int n = points.size();
MatrixXd dist(n, n);
for(int i = 0; i < n; i++)
for(int j = i; j < n; j++)
dist(i, j) = dist(j, i) = (points[i] - points[j]).norm();
return dist;
}
MatrixXd calc_relative_error(const MatrixXd& mat1, const MatrixXd& mat2)
{
assert(mat1.rows() == mat2.rows() && mat1.cols() == mat2.cols());
const int rows = mat1.rows();
const int cols = mat1.cols();
MatrixXd result(rows, cols);
for(int i = 0; i < rows; i++)
for(int j = 0; j < cols; j++)
result(i, j) = i - j ? (mat1(i, j) / mat2(i, j)) : 0;
return result;
}
template<class T, class Iter>
void calc_statistics(Iter begin, Iter end, std::ostream& os)
{
using namespace boost::accumulators;
accumulator_set<double, features<tag::min, tag::max, tag::mean, tag::variance> > acc;
for(; begin != end; ++begin) acc(*begin);
//いろいろ表示したいなら
//os << "平均:" << extract::mean(acc) << std::endl;
//os << "標準偏差:" << std::sqrt(extract::variance(acc)) << std::endl;
//os << "最大:" << extract::max(acc) << std::endl;
//os << "最小:" << extract::min(acc) << std::endl;
os << "sigma/mu = " << std::sqrt(extract::variance(acc)) / extract::mean(acc) << std::endl;
}
void calc_statistics_of_points(const std::vector<Eigen::VectorXd>& points, std::ostream& os = std::cout)
{
std::vector<double> t(points.size());
std::transform(points.begin(), points.end(), t.begin(), [](const Eigen::VectorXd& p){ return p.norm(); });
calc_statistics<double>(t.begin(), t.end(), os);
}
void calc_statistics_of_distance(const MatrixXd& mat, std::ostream& os = std::cout)
{
const int rows = mat.rows();
const int cols = mat.cols();
std::vector<double> t;
for(int i = 0; i < rows; i++)
for(int j = i + 1; j < cols; j++)
if(1e-6 < mat(i, j))
t.push_back(mat(i, j));
calc_statistics<double>(t.begin(), t.end(), os);
}
<br />
int main()
{
boost::mt19937 gen(static_cast<unsigned long>(time(0)));
boost::uniform_real<> dst_uniform(-1, 1);
boost::variate_generator< boost::mt19937&, boost::uniform_real<> > rand_uniform(gen, dst_uniform);
boost::normal_distribution<> dst_normal(0, 1);
boost::variate_generator< boost::mt19937&, boost::normal_distribution<> > rand_normal(gen, dst_normal);
auto rand_helsinki = [&gen](){
int t(gen() % 6);
if(t == 0) return std::sqrt(3);
else if(t == 1) return -std::sqrt(3);
else return 0.0;
};
auto rand_sparse = [&rand_uniform](){
constexpr double density = 0.01;
if(fabs(rand_uniform()) < density)
return rand_uniform();
else
return 0.0;
};
const std::vector<int> ks = {100, 500, 1000}; //点群の数
const std::vector<int> Ms = {100, 1000, 10000}; //次元
const std::vector<double> rs = {0.01, 0.02, 0.05, 0.1, 0.2}; //削減率
for(double r: rs)
{
std::cerr << "削減率:" << (r * 100) << "%" << std::endl;
for(int M: Ms)
{
int N = static_cast<int>(r * M);
for(int k: ks)
{
//ここに渡すのを切り替えることで変換行列生成方法を変えます><
const MatrixXd R = gen_projection_matrix(M, N, rand_sparse);
const std::vector<Eigen::VectorXd> srcs = gen_random_points(M, k, gen);
const std::vector<Eigen::VectorXd> dsts = projection_points(M, N, R, srcs);
const MatrixXd src_dist = gen_distance_vector(srcs);
const MatrixXd dst_dist = gen_distance_vector(dsts);
const MatrixXd relative = calc_relative_error(src_dist, dst_dist);
/*
//距離行列と距離変化率行列の表示
std::cerr << src_dist << std::endl << std::endl;
std::cerr << dst_dist << std::endl << std::endl;
std::cerr << relative << std::endl << std::endl;
*/
/*
//生成点群が球面上に分布してることがわかります
std::cerr << "元の点群の原点からの距離の分布" << std::endl;
calc_statistics_of_points(srcs, std::cerr);
//変換後の点群はそれほどではありませんがやはり球面付近に分布しています
std::cerr << "変換後の点群の原点からの距離の分布" << std::endl;
calc_statistics_of_points(dsts, std::cerr);
*/
std::cerr << M << "次元 -> " << N << "次元";
calc_statistics_of_distance(relative, std::cerr);
}
}
}
}
実験2:SIFT特徴量の次元削減による画像間対応付け
詳細は述べませんが,SIFTという局所特徴量があり,ある点を中心として最もその点の特徴をよく表す範囲の様子を回転・スケーリング・照明変動に頑健な形で128次元ベクトルで記述する手法があります.
1枚の画像からたくさんのSIFT特徴量(たいてい数百から数千点),すなわち128次元の点群を求めると,別の画像から同様に得た特徴量との最近傍探索によって異なる画像の2点が同一のものを写してると判断できる…というようなものです.
たぶん128次元といったらそれほど高次元じゃないので,Random Projectionの実験としてはそれほど適切じゃないかもしれない.
超劇的な効果ってことはないとおもいます.
プログラムの概要
2枚の画像を読み込んで,それぞれからSIFT特徴量を得ます.
この特徴量同士の対応付けを128次元のまま行った場合と,順に64次元,32次元,16次元,8次元に落とした場合で比べてみます.
実装
OpenCV 2.3.1aを使っています.
OpenCVのSIFT Descriptorで抽出された128次元の特徴量群はcv::Matによって(特徴点数)行×128列の行列として記述され,その各行がひとつの特徴量を表します.これを変換して,(特徴点数)行×(落とした次元数)列の行列をつくり,あとはOpenCVにまかせて最近傍探索による対応付けを行います.
プログラムを実行するには,画像ファイル名をふたつ,落とす次元数を指定します.
SIFTの特徴量そのままでの対応付け結果を”128.jpg”に,次元を落として対応付けた結果を”N.jpg”に出力しています.
なおエラーチェックの類は一切行っていません.
以下コンパイルから実行まで.
% g++ prog.cpp -Wall -O2 -std=c++0x -I/usr/local/include/opencv -I/usr/local/include/eigen3 -lopencv_features2d -lopencv_core -lopencv_highgui % ./a.out img1.jpg img2.jpg 32 % display 128.jpg % display N.jpg
実行例
面倒なので定量的な評価は行いません.
性能評価も行いません.
ぱっと見ちゃとできてるのでよしとします.
同じ画像での対応付け
これがちゃんとできてるのは当然ですw
回転・スケーリング画像での対応付け
256×256のLennaをだいたい45度くらい傾けて縮小したものです.
そこそこいけてないですか?
プログラム
ソースぜんぶ載せます.コンパイル方法は上にちょっと書いた通り.
#include <vector>
#include <eigen3/Eigen/Core>
#include <opencv2/opencv.hpp>
#include <opencv2/core/core.hpp>
#include <opencv2/core/eigen.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <boost/lexical_cast.hpp>
#include <boost/random.hpp>
<br />
//※行列生成はほぼ上のシミュレーション実験のと同じですが,
// MatrixXdじゃなくてMatrixXfにしてあります.
template<class T>
Eigen::MatrixXf gen_projection_matrix(int N, int D, T& rand)
{
Eigen::MatrixXf mat(D, N);
for(int i = 0; i < N; i++)
for(int j = 0; j < D; j++)
mat(j, i) = rand();
return mat;
}
cv::Mat random_projection(const cv::Mat& dsc, const Eigen::MatrixXf& R)
{
const int rows = dsc.rows;
cv::Mat result(rows, R.rows(), CV_32FC1);
for(int r = 0; r < rows; r++)
{
//行をとってきてEigenのベクトルに変換
cv::Mat row = dsc.row(r);
Eigen::MatrixXf row_eigen;
cv::cv2eigen(row, row_eigen);
//Rによる射影
row_eigen = (R * row_eigen.transpose()).transpose();
//cv::Matに戻す
//※領域的なごちゃごちゃで手作業コピーしてます;;
for(int i = 0; i < R.rows(); i++)
result.at<float>(r, i) = row_eigen(i);
}
return result;
}
<br />
int main(int argc, char *argv[])
{
if(argc != 4)
return -1;
//Random Projectionの行列生成方法の一覧
boost::mt19937 gen(static_cast<unsigned long>(time(0)));
boost::uniform_real<> dst_uniform(-1, 1);
boost::variate_generator< boost::mt19937&, boost::uniform_real<> > rand_uniform(gen, dst_uniform);
boost::normal_distribution<> dst_normal(0, 1);
boost::variate_generator< boost::mt19937&, boost::normal_distribution<> > rand_normal(gen, dst_normal);
auto rand_helsinki = [&gen](){
int t(gen() % 6);
if(t == 0) return std::sqrt(3);
else if(t == 1) return -std::sqrt(3);
else return 0.0;
};
auto rand_sparse = [&rand_uniform](){
constexpr double density = 0.01;
if(fabs(rand_uniform()) < density)
return rand_uniform();
else
return 0.0;
};
//変換行列生成(上のrand_*のどれか)
const int N = boost::lexical_cast<int>(argv[3]);
const Eigen::MatrixXf R = gen_projection_matrix(128, N, rand_uniform);
//SIFT関係
cv::SiftFeatureDetector detector;
cv::SiftDescriptorExtractor extractor;
cv::BruteForceMatcher<cv::L2<float> > matcher;
//画像読み込み
cv::Mat img1 = cv::imread(argv[1]);
cv::Mat img2 = cv::imread(argv[2]);
//画像1から特徴量抽出
std::vector<cv::KeyPoint> kps1;
cv::Mat dsc1;
detector.detect(img1, kps1);
extractor.compute(img1, kps1, dsc1);
//画像2から特徴量抽出
std::vector<cv::KeyPoint> kps2;
cv::Mat dsc2;
detector.detect(img2, kps2);
extractor.compute(img2, kps2, dsc2);
//128次元をN次元に落とす
cv::Mat dsc1_N = random_projection(dsc1, R);
cv::Mat dsc2_N = random_projection(dsc2, R);
std::vector<cv::DMatch> matches_N;
matcher.match(dsc1_N, dsc2_N, matches_N);
cv::Mat result_N;
cv::drawMatches(img1, kps1, img2, kps2, matches_N, result_N);
//128次元のSIFT特徴量そのままで最近傍探索
std::vector<cv::DMatch> matches128;
matcher.match(dsc1, dsc2, matches128);
cv::Mat result128;
cv::drawMatches(img1, kps1, img2, kps2, matches128, result128);
cv::imwrite("128.jpg", result128);
cv::imwrite("N.jpg", result_N);
}
まとめ
こういうのはほんとおもしろいですね.
もっと理論的に詰めて理解したいんですけども.
ツッコミどころはたくさんあると思いますので,容赦なくお願い致します.