おさかなおさかなって言ってたらリアルにお魚好きになってしまったって話は前もしたと思うんですが，そのせいでホントに魚が食べたい今日このごろです．調理法としては，お刺身の次点くらいで焼き魚と酒蒸しが好きです．お刺身はそのままスーパーで買ってくればいいし（美味しいかと言われると微妙ですが），焼き魚も買ってきてグリルで焼くだけなので気軽にできるんですが，酒蒸しはちょっと自宅ではできなくて食卓が寂しいです．

さて，C++11では乱数関連のライブラリについてもboost由来の大幅強化がされまして，ホントに強力なものになっています．
まず乱数エンジンでは，よりよい擬似乱数アルゴリズムが豊富に取り揃えられており，さらにはハードウェアを利用した真の乱数も扱えます．
また生成される乱数の分布の点でも，通常の一様分布や各種の確率分布（GaussianやPoissonなど）が利用できます．

今日お話するのは分布の中でも，出力される各値の確率をユーザが指定できるノンパラメトリックな分布を実現するstd::discrete_distributionのお話．

なおboost::randomからstd::randomへは大きな設計変更がありましたけれども，今回の話に関しては普通にstd::discreted_distributionをboost::random::discrete_distributionとそのまま読み替えてもらっても大丈夫です．

やりたいこと

おみくじプログラムを作りましょう．

• 大吉：1%
• 中吉：9%
• 小吉：25%
• 吉：25%
• 末吉：30%
• 凶：9%
• 大凶：1%

という出現確率とします．

ベタにやると，0〜99までの一様乱数を生成し，どの範囲に属するか自分で判定することになるのではないでしょうか．

出力例はこんなかんじ．確かに小吉や吉や末吉が多いですね．これ見てるとゲシュタルト崩壊してきてあかん・・・

小吉 吉 凶 小吉 小吉 吉末 小吉 大凶 大凶 凶 吉 凶 小吉 吉 小吉 大吉 小吉 吉 吉 吉末 吉 吉末 小吉 吉 吉末 吉 吉末 吉末 小吉 小吉

これは記述量だけでもなかなかめんどくさいし，出現確率の累積とか乱数値から真に欲しい値に変換する辺りとかパッと見何してるかぜんぜんわからないですね．
これをバシッとやってくれるのがstd::discrete_distributionです．

std::discrete_distributionを使ってみよう

std::discrete_distributionは，次のような分布の乱数を生成する分布エンジンです(*1)．

式を見ての通り，は重みなので確率である必要はなく要するにである必要がありません．

重みは整数型の必要があります．

ということで，おみくじプログラムをstd::discrete_distributionを使って書き直すと次のようになります．

このとおり一気にすっきりしましたし，乱数が直接そのまま欲しい分布になってて変換する必要がない辺りはとても助かります．

分布（重み）の与え方にはいくつかあって，上に書いたやり方に加えて例えば

std::discrete_distribution<int> dst = {1, 2, 3, 4};

という書き方なら重みが完全に定数ならさらにすっきり書けます．

std::piecewise_constant_distribution

std::discrete_distributionの応用的なものとしてstd::piecewise_constant_distributionがあります．

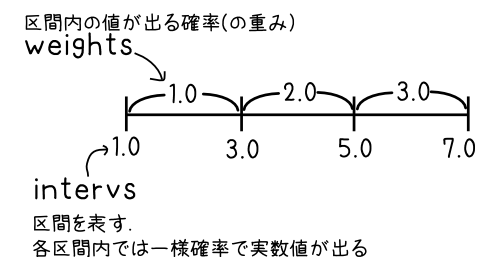
これは，生成する値が一定区間内で一様分布するアナログ値（実数値）となり，その区間に出る確率を重みが表すものです．

次のようなコードを書くと

std::vector<double> weights = {1, 2, 3};
std::vector<double> intervs = {1, 3, 5, 7};
std::piecewise_constant_distribution<double> dst2(intervs.begin(), intervs.end(), weights.begin());

hoge = dst2(rng);

これはこのような分布を表します．

なので，出力される値の例は

6.70997 4.61671 6.45071 5.48144 2.43457 4.83174 4.04132 5.11937 5.8644 6.95352 5.88197 6.65031 5.02199 5.23308 5.01276 4.77485 5.18637 4.68551 6.4178 5.41693 4.99127 6.9197 1.41181 6.90801
 4.17912 5.71808 4.0774 6.4235 1.54071 5.64048 5.99976 2.59595 6.92944 2.14426 3.69604 6.20845 1.93068 5.50954 1.09713 5.72115 5.13573 4.632 3.19731 2.65602 4.294 6.04969 1.48565 3.51774 
5.01908 6.29042 6.92689 6.29382 3.81096 1.57533 3.48709 5.17622 6.5509 4.06304 1.39922 2.95447 6.50946 3.26181 3.63652 4.95465 3.34052 4.94181 6.81977 5.60787 6.03001 4.61147 5.21152 
1.63783 3.93506 4.42989 6.63373 6.23655 3.54978 2.55816 4.95996 4.271 5.87388 3.72683 5.49374 6.2475 3.87505 4.31426 4.06358 6.26308 5.67714 4.27651 4.75098 3.82168 6.64226 4.93171 6.02316
 2.29674 4.36154 6.48075 4.16516 6.66847

という風になります（5以上7未満の値が一番たくさん出ていることがわかりますね）

おさかなさん的には今の段階ではまだ具体的な用途を思いつきませんが何かに使えそう感はあります！ｗ　←

std::piecewise_linear_distribution

基本的には上で述べたstd::piecewise_constant_distributionとよく似ています．

constantがlinearになったことから想像がつくかと思いますが，各区間内での分布が両隣の区間の出現確率に併せてリニアに変化するような分布です．

std::piecewise_constant_distributionの確率密度関数は階段状の形になりますが，std::piecewise_linear_distributionの確率密度関数は斜めの線分をつなぎあわせたような形になるわけです．

これによって，原理的には無限の自由度のノンパラメトリック分布な乱数を生成できるようになるわけですね．
リニアじゃなくて二次補間とかもできるのがあればもっといいかも？ｗ めちゃくちゃ難しそうだけど

（ちょっとここの説明，お茶を濁してる感はんぱないすね・・・ｗ　←

生成される確率だけでなく値自体もカスタムしたい

たとえばおみくじの場合std::discrete_distributionが生成するのは文字列配列の添字なので0から始まる整数で十分でした．

出てくる値も0から始まる整数だけでなく，例えば100と200と500を適当な確率で出すようにしたい，などのカスタムは直接記述する手段はなく，出力される値の配列を事前に用意しておいてそれを経由することになるでしょう．
（むしろおみくじプログラムでやってることはそれに他ならないですね）

まとめ

乱数が欲しい場合でも，常に一様乱数や各種の有名なパラメトリック確率分布で事足りるわけではないという例を示し，それをstd::discrete_distributionの機能で華麗に解決してみました．

std::piecewise_*_distributionについてもいい例を考えたかったんですがそこはまた気が向いたらということで．

乱数，大事です．